Chapter 6.1

In class today, we discussed a few things about angles. We discussed them in terms of degrees, different ways of expressing degrees, how degrees relate to radians, and how to convert the two using dimensional analysis.So, let us take a more in-depth look.

Angle--two rays with a common end point

Degrees--a measure of rotation (TRIVIA: Derived from Babylonian belief that it takes the sun 360 days to orbit the Earth)

Magnitude--value

Vector--value with direction

Angular Speed--degrees/time (RPMs or Revolutions Per Minute are one example)

Linear Speed--distance of outer most rotating part/time


Quadrant Angles--instances in which the terminal side is on an axis

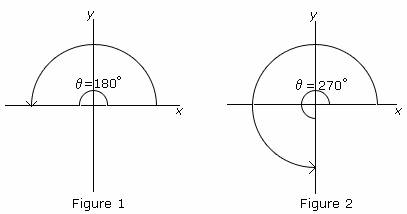
*NOTE--Not on any quadrant, but between them
Radian--The amount of rotation of the radius such that the intersected arc is the same length as the radius
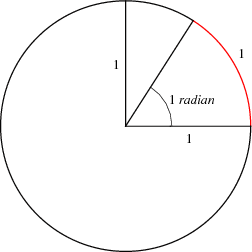
*NOTE--Because of what we know about the relationship between the radius of a circle and it's circumference, we know that there are 2π radians in a circle. (From the formula C=2πr)


Initial Side--the starting ray from which the rotation is measured
Terminal Side--the ray that ends the measurement of the rotation
Standard Posistion--the vertex of the angle lies on the origin

Co-terminal--when two angles share the same terminal side.


This wonderful picture shows us an angle that looks simple having many measurements. Because the rotation always ends on the same terminal angle, these are co-terminal. Notice also how there can be infinitely many co-terminal angles because one can always add or subtract 360 degrees.

Positive Degrees--Degrees measured positively are always going counter-clockwise from the initial side.
Negative Degrees--Always going clockwise from terminal side
(also shown in picture above)

Conversions:
Degrees to radians:

This is simple proportion work. We know that in the whole of a circle, we have 360 degrees. We also know that we have 2π radians in a circle. So we put it in a fraction and reduce it to π over 180, and multiply by the angle we are trying to convert.
The opposite, getting it from radians into angles works the same way, just by cross multiplying and cancelling. Simple. For now.


The last thing I'll cover will be the different units of measuring degrees. Some men just wanna watch the world burn, and for this reason, we have  more than one way of measuring degrees.
Standard-32.50°
Minutes/Seconds-- This is how one converts. The whole number remains the same:
32°
It's the decimal that needs to be converted. So, to get minutes, we take .50 and multiply it by 60, which ends up being 30. So we have 30 minutes.
32° 30'
Which terminates fairly simply. If there are decimals in the minutes product, you multiply that by 60 to get seconds.
To convert it the other way you divide the minutes and seconds by 60, reversing the change.
32°
30/60=.50
32.50°


Not in a spring sport? Try the Ultimate Frisbee Club!
HAPPY BIRTHDAY, ERIN JACOBS!


Well, that was great fun. I wish every one in this class godspeed. Remember that life is a lot simpler when you keep your head up and eyes forward.
Shane McPartlin
P.S.