10.2: Arithmetic Sequences

An Arithmetic Sequence is a sequence that has a common difference (d) between each term.

For any numbers/terms j and k. Arithmetic Sequences are linear, they increase by the same amount each term. Finding the Common Difference (d):

Don't be afraid to do it in your head... Examples: -3, 2, 7, 12, ... Common Difference = +5 17, 10, 3, -4, ... Common Difference = -7 The common difference is constant!!! This means that it always stays the same no matter what two consecutive terms next to each other that you measure the difference of. Another way to look at it is this:

You can also use that to prove that the sequeuence is infant arithmetic. Finding the nth term of an arithmetic sequence:

Example: Find the 63rd term of a sequence when d=4 and the first term is 12.

Therefore the 63rd term would be 260. This works because you are taking the starting point plus the common difference time the term you need minus one, so that you don't count the first term as zero. Finding the Sum:

n is the number of the terms that you are finding the sum of. But first you must find a sub n with that formula. The Partial Sum can also be defined as:

Example: Find the sum: First term=40 d=-3 n=30

Therefore the partial sum is -105. You may also see it in summation notation:

The top stands for the top limit of the partial and the bottom is the lower limit. a sub n is the formula for any term in the sequence. Jacob Kalt

10.1 Sequences and Summation Notation

A sequence is a function whose domain is all natural numbers.

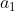 represents the first time of the sequence, while  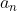denotes a positive integer, or the nth term.
Sequences often appear as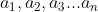  , representing the first three terms of the sequence, as well as the nth term.

An infinite sequence is a function whose domain is the set of positive integers.

For example: Find the eighth term of the sequence,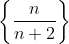  with the first four terms: 1/3, 1/2, 3/5, 2/3...
Eighth term:
 n=8
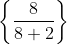= 4/5

There are two basic forms of writing sequences, recursive  and explicit.


Recursive Form






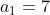
On the other hand, the same sequence may be represented in this way as well:

Explicit Form




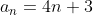
Summation Notation
Summation notation is another alternative form of a sequence that can be used to find the sum of multiple terms of an infinite sequence.

Summation Notation
 

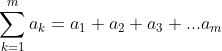
k represents the lower limit, while m represents the upper limit.
k also represents the index of summation.

This picture also re-explains summation notation in slightly different terms.


There are also two rules that apply to the sums of a constant.

Theorems on the Sum of a Constant:

1)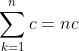 (c being a constant)


2)


There are also a few theorems that derive from the following original theorem on sums.

Theorem on Sums


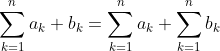Addition

Subtraction


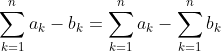
Constants
 for every real number c


To evaluate a sum:

Find the sum:



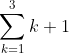
To find the sum, substitute the integers 1 (lower limit) through 3 (upper limit) in for k and add the resulting terms together.

(1+1) + (2+1) + (3+1)= 9

That's it for now, thank you!

Julia Wilkins

9.7 The Inverse of a Matrix

We've been learning about matrices for a while so lets learn about the inverse of a matrix.

Important: You can only have inverses of square matrices (2x2, 3x3).

Quick Review:
An identity matrix is a matrix with ones in the main diagonal and zeros for all the other elements.

Definition of an Inverse Matrix- 

Matrix A multiplied by the inverse of matrix A equals the identity of matrix A also is equal to the inverse of matrix A multiplied by matrix A.

If a square matrix has an inverse it is known as Invertible

Finding the Inverse of a Matrix

Lets find the inverse of matrix A.

The first thing we need to do is augment (or add) the multiplicative identity of A so 

Now we want to switch the left side to the identity of A by using elementary row transformations.

We have changed the left side into the identity so the right side is now the inverse

To verify the inverse plug it into

and get 

You can use this method for square matrices or just use a graphing calculator.

Solving Systems of Linear Equations

-x+3y+z=1

2x+3y=3

3x+y-2z=-2

First set up 3 matrices

Then multiply by the inverse of A

and 

so

Example from the book

Heres a link to a helpful video

http://www.youtube.com/watch?v=r9aTLTN16V4&feature=plcp

-Tommy McLeod

Thanks to geller for letting me use his account

9.6 The Algebra of Matrices

Hey guys!

So we're all pretty practiced when it comes to algebra and real numbers, but how about we focus on algebra of matrices. 

Really quick refresher: 

Matrix- one

Matrices- two or more

Elements- numbers within or that make up the matrix

The dimensions of a matrix are # of rows by #of columns

An element is identified by the row and column it is in

The Actual Thing

Addition of Matrices

- Two matrices can be added only if they have the same size

- Add the elements in corresponding positions of each matrix

Ex:

-The m x n zero matrix or additive identity is a matrix with all elements = 0

Such as: 

OR

OR

...you get the point

-The additive inverse of a matrix A is obtained by changing the sign of each nonzero element of matrix A

So:

The additive inverse of 

is

-Theorem on Matrix Properties

If A, B, and C are m x n matrices and if O is the m x n zero matrix

1.  A+B = B+A

2. A+ (B+C) = (A+B) + C

3. A+O = A

4. A + (-A) = O

Subtraction of Matrices

- Subtraction is pretty simple if you understand addition

we simply treat   A-B    as    A+(-B)

- just as in addition we subtract the elements in corresponding positions

Multiplication of Matrix

-When multiplying a real number  c  by a matrix A  you multiply each element of A by c 

EX:

100 200 300 400

=    A

                                                                                 5      =    C

5

100 200 300 400

=

5 * 100 5 * 200 5 * 300 5 * 400

=

500 1000 1500 2000

-Theorem On Matrix Properties

If A and B are m x n matrices and if c and d are real numbers, then

1. c(A+B) = cA + cB

2. (c+d)A = cA + cdA

3. (cd)A = c(dA)

Multiplication of Matrices

-When multiplying to matrices, the number of columns in the first matrix must = the number of rows in the second matrix

(remember dimensions of a matrix are rows x columns)

- Because of that

if the 1st matrix is 2 x 3 

and the 2nd matrix is 3 x 5

the resulting matrix will be 2 x 5

- When multiplying two matrices an element in row 1 column 1 is equal to row 1 of the first matrix multiplied by column 1 of the second matrix

So:

if

and

then 

- Something thats important to remember is that

The book gives a good explanation and example of this. and I'm getting pretty sick of typing everything up, so here

-If you still need help with Matrix Multiplication here is a website that explains it in yet another way, I found it very helpful and easy to understand:

http://www.mathsisfun.com/algebra/matrix-multiplying.html

and if you are more of an auditory learner heres a nice little video from Khan Academy

http://www.khanacademy.org/math/algebra/algebra-matrices/v/matrix-multiplication--part-1

actually its on the longer side but hey #firstworldstruggz
#ijustusedahashtag  #eww

-Almost done, okay multiplicative identities are always squared. They are also in reduced echelon form!
SO: the multiplicative identity for a 2x2 matrix would be

the multiplicative identity for a 3x3 would be 

And so on..

So that's what's up with Algebra of Matrices. 

People may doubt what you say

but they will believe what you do.

That's what the fortune cookie I just ate said. Deep. You can go ponder that now.

Oh and just cause I'm a pushy business woman, heres the link to my itunes: http://itunes.apple.com/us/album/leah-lavigne-ep/id480771601

-Leah